Возьмём отрезок a . Чтобы найти его длину, выберем в качестве единицы длины отрезок е. (рис. 1) При

измерении оказалось, что длина отрезка е

а больше 3 е , но меньше 4 е . Поэтому её е1

нельзя выразить натуральным числом рис 1

(при единице длины е ). Но если разбить отрезок е на 4 равные части, каждая из которых равна е 1 , то длина отрезка а окажется равной 14е1 . Если же вернуться к первоначальной единице длины е , то мы должны сказать, что отрезок а состоит из 14 отрезков, равных четвёртой части отрезка е , т.е., говоря о длине отрезка а , мы вынуждены оперировать двумя натуральными числами 14 и 4 . Условились в такой ситуации длину отрезка записывать в виде 14/4 е , а символ называть дробью.

В общем виде понятие дроби определяют так: пусть даны отрезок а и единичный отрезок е , причём отрезок е является суммой n отрезков, равных е 1 . Если отрезок а состоит из m отрезков, равных е 1 , то его длина может быть представлена в виде е . Символ называют дробью, в нём m и n - натуральные числа. Читают этот символ «эм энных».

Вернёмся к рис.1 . Выбранный отрезок е 1 есть четвёртая часть отрезка е . Очевидно, что это не единственный вариант выбора такой доли отрезка е , которая укладывается целое число раз в отрезке а . Можно взять восьмую часть отрезка е , тогда отрезок а будет состоять из 28 28/8 е . Можно взять шестнадцатую часть отрезка е , тогда отрезок а будет состоять из 56 таких долей и его длина будет равна е . Если представить себе этот процесс продолженным неограниченно, получим, что длина отрезка а может быть выражена бесконечным множеством различных дробей: 14/4, 28/8 , 56/16 ,…

Вообще, если при единице длины е длина отрезка а выражается дробью, то она может быть выражена любой дробью, где k- натуральное число.

Определение. Дроби, выражающие длину одного и того же отрезка при единице длины е , называют равными дробями.

Если дроби и равны, то пишут: = . Например, дроби 14/4 и 28/8 выражают длину одного и того же отрезка при единице длины е , следовательно, 14/4 = 28/8 .

Существует признак, пользуясь которым определяют, равны ли данные дроби:

Для того, чтобы дроби m / n и p / q были равны, необходимо и достаточно, чтобы mq = np.

1. Покажем, что m / n = p / q => mq = np . Так как m / n = p / q для любого натурального q , а p / q = pn / qn для любого натурального n , то, из равенства дробей m / n и p / q следует равенство mq / nq = pn / qn , из которого в свою очередь вытекает, что mq = np .

2. Покажем, что mp = pq => m / n = p / q . Если разделить обе части истинного равенства mq = np на натуральное число nq , то получим истинное равенство mq / nq = np / nq . Но mq / nq = m / n , а np / nq = p / q , => m / n = p / q .

Пример.Определим, равны ли дроби 17/19 и 23/27 . Для этого сравним произведения 17*27 и 19*23 ; 17*27=459 , 19*23=437 . Так как 459 ¹ 437 , то 17/19 ¹ 23/27.

Из рассмотренных ниже фактов вытекает основное свойство дроби:

Если числитель и знаменатель данной дроби умножить на одно и тоже натуральное число, то получится дробь, равная данной.

На этом свойстве основано сокращение дробей и приведение дробей к общему знаменателю.

Сокращение дробей- это замена данной дроби другой, равной данной, но с меньшим числителем и знаменателем.

Если числитель и знаменатель дроби одновременно делятся только на единицу, то дробь называют несократимой . Например, 3/19 - несократимая дробь.

Пример. Сократим дробь 48/80 . Чтобы получить равную ей несократимую дробь, необходимо числитель и знаменатель данной дроби разделить на их наибольший общий делитель. Найдем его: Д (48;80 ) = 16 . Разделив 48 на 16 и 80 на 16 , получаем, что 48/80 = 3/5. Дробь 3/5 - несократимая.

Приведение дробей к общему знаменателю- это замена дробей равными им дробями, имеющими одинаковые знаменатели.

Общим знаменателем двух дробей m / n и p / q является общее кратное чисел n и q , а наименьшим общим знаменателем- их наименьшее общее кратное К (n , q ).

Пример. Приведём к НОЗ дроби 8/15 и 4/35. Разложим числа 15 и 35 на простые множители: 15 =3*5 , 35 =5*7 . Тогда К (15,35 )=3*5*7 =105 . Поскольку 105=15*7=35*3 , то = 8/15 = 8*7/15*7 = 56/105, 4/35 = 4*3/35*3 = 12/105 .

Сложение и вычитание

Пусть отрезки a , b , c таковы, что c = a + b и при выбранной единице длины e a = е, b= e (рис.2). тогда c = a + b = e + e = 6 e 1 = 7 e 1 = (6+7)*е 1 = 13е 1 = е 1 , т.е. длина отрезка е выражается числом, которое целесообразно рассматривать, как сумму чисел 6/4 и 7/4 .

Определение: Если положительные рациональные числа представлены дробями m/n и p/n , то суммой чисел a и b называется число, представляемое дробью m+p/n .

m/n + p/n = m+p/n (1)

Если положительные рациональные числа представлены дробями с разными знаменателями, то эти дроби приводят к НОЗ , а потом складывают по правилу (1 ). Например: 5/12+2/15=25/60+8/60=25+8/60=33/60=11/20 .

Сумма любых двух положительных чисел существует и единственна. Сложение положительных рациональных чисел подчиняется переместительному и сочетательному законам:

a+b=b+a для любых a,b, Î Q+

(a+b)+c = a+(b+c) для любых a,b,c Î Q+

Различают правильные и неправильные дроби. Дробь называют правильной, если её числитель меньше знаменателя, и неправильной, если её числитель больше знаменателя или равен ему.

Пусть m / n - неправильная дробь. Тогда m ³ n . Если m кратно n ,то в этом случае дробь m / n является записью натурального числа. Например, если дана дробь 15/3 , то 15/3 =5 . Если число m не кратно n , то разделим m на n с остатком: m = nq + r , где r < n . Поставим nq + r вместо m в дробь m / n и применим правило (1): m / n = nq + r / n = nq / n + r / n = q + r / n .

Поскольку r < n , то дробь r / n правильная => дробь m / n оказалась представлена в виде суммы натурального числа q и правильной дроби r / n . Это действие называют выделением целой части из неправильной дроби. Например, 13/4=4*3+1/4=4*3/4+1/4=3+1/4. Принято сумму натурального числа и правильной дроби записывать без знака сложения, т.е вместо 3+1/4 пишут 3 1/4 и называют такую запись смешанным числом.

Рассмотрим вычитание положительных рациональных чисел.

Определениe Разностью положительных рациональных чисел a и b называется такое положительное рациональное число c, что a=b+c

Понятие разности определено, а как практически из одного положительного рационального числа вычесть другое?

Пусть a = m / n , b = p / n , а разность а- b пусть представляется дробью x / n . Найти x . По определению разности m / n = p / n + x / n , а по правилу (1) p / n + x / n = p + x / n . Таким образом, m = p + x , но m , p и x _числа натуральные, а для них эта запись означает, что x = m — p .

Приходим к следующему правилу:

M/n-p/n=m-p/n (2)

Умножение и деление

На рис.3 приведены такие отрезки: a, e, и e1, что a=11/3 e; e=6/5 e1. Надо узнать, каким будет значение длины данного отрезка а при единице длины е1. Так как 3 a =11 e, а 5е=6е1 , то, умножив первое равенство на 5, а второе на 11 , получим 5*3а=11*5е и 11*5е=6*11е1, или 15а=66е1. Последнее равенство означает, что а=66/15е1 , т.е. длина отрезка а при единице длины е1 выражается числом 66/15 , которое целесообразно рассматривать как произведение 11/3 и 6/5.

Определение Если положительные рациональные числа представлены дробями m/n и p/q, то их произведение есть число, представленное дробью mp/nq

m/n*p/q=mp/nq (3)

Определение Частное двух положительных рациональных чисел a и b называется такое число с, что a=b*c. Частное двух положительных рациональных чисел находят по формуле:

m/n:p/q=mq/np (4)

Заметим, что знак черты в записи дроби m/ n можно рассматривать как знак действия деления. Действительно, возьмем два натуральных числа m и n , и найдем их частное по правилу (4):

m:n=m/1:n/1=m*1/n*1=m/n

Обратно, если дана дробь m / n , то m / n = m *1/ n *1 . Так как m / n = m : n , то любое положительное рациональное число можно рассматривать как частное двух натуральных чисел. Кстати, термин «рациональное число» произошел от латинского слова ratio , что в переводе на русский язык означает «отношение» (частное).

1.Сложение и вычитание дробей с одинаковыми знаменателями

При сложении дробей с одинаковыми знаменателями числители складывают, а

При вычитании дробей с одинаковыми знаменателями из числителя первой дроби вычитают числитель второй дроби, а знаменатель оставляют тот же.

Примеры: а) ; б)

2.Сложение и вычитание дробей с разными знаменателями

Чтобы сложить (вычесть) дроби с разными знаменателями, надо:

привести данные дроби к наименьшему общему знаменателю

сложить (вычесть) полученные дроби (как в пункте1)

Примеры: а)
; б)

3.Сложение и вычитание смешанных чисел

Чтобы сложить смешанные числа, надо:

привести дробные части этих чисел к наименьшему общему знаменателю;

отдельно выполнить сложение целых частей и отдельно дробных частей. Если при сложении дробных частей получилась неправильная дробь, выделить целую часть из этой дроби и прибавить ее к полученной целой части.

Примеры: а)
; б)

Чтобы выполнить вычитание смешанных чисел, надо:

привести дробные части этих чисел к наименьшему общему знаменателю; если дробная часть уменьшаемого меньше дробной части вычитаемого, превратить ее в неправильную дробь, уменьшив на единицу целую часть;

отдельно выполнить вычитание целых частей и отдельно дробных частей.

Примеры: а)
; б)

4.Умножение дробей

а) Чтобы умножить дробь на натуральное число , надо ее числитель умножить на это число, а знаменатель оставить без изменения

Примеры:

б) Чтобы умножить дробь на дробь , надо:

1) в числителе записать произведение числителей, в знаменателе – произведение знаменателей;

2) выполнить сокращение (если возможно);

3) выполнить умножение

Примеры: а)
; б)

в) Для того, чтобы выполнить умножение смешанных чисел, надо их записать в виде неправильных дробей, а затем воспользоваться правилом умножения дробей.

Примеры:

5.Деление дробей

Чтобы разделить одну дробь на другую, надо делимое умножить на число, обратное делителю

Эта статья представляет собой общий взгляд на действия с дробями. Здесь мы сформулируем и обоснуем правила сложения, вычитания, умножения, деления и возведения в степень дробей общего вида A/B , где A и B некоторые числа, числовые выражения или выражения с переменными. По обыкновению материал будем снабжать поясняющими примерами с детальными описаниями решений.

Навигация по странице.

Правила выполнения действий с числовыми дробями общего вида

Давайте договоримся под числовыми дробями общего вида понимать дроби, в которых числитель и/или знаменатель могут быть представлены не только натуральными числами, но и другими числами или числовыми выражениями. Для наглядности приведем несколько примеров таких дробей: , .

Нам известны правила, по которым выполняются . По этим же правилам можно выполнять действия с дробями общего вида:

Обоснование правил

Для обоснования справедливости правил выполнения действий с числовыми дробями общего вида можно отталкиваться от следующих моментов:

• дробная черта - это по сути знак деления,
• деление на некоторое отличное от нуля число можно рассматривать как умножение на число, обратное делителю (этим сразу объясняется правило деления дробей),
• свойств действий с действительными числами ,
• и его обобщенном понимании ,

Они позволяют провести следующие преобразования, обосновывающие правила сложения, вычитания дробей с одинаковыми и разными знаменателями, а также правило умножения дробей:

Примеры

Приведем примеры выполнения действия с дробями общего вида по разученным в предыдущем пункте правилам. Сразу скажем, что обычно после проведения действий с дробями полученная дробь требует упрощения, причем процесс упрощения дроби часто сложнее, чем выполнение предшествующих действий. Мы не будем подробно останавливаться на упрощении дробей (соответствующие преобразования разобраны в статье преобразование дробей), чтобы не отвлекаться от интересующей нас темы.

Начнем с примеров сложения и вычитания числовых дробей с одинаковыми знаменателями. Для начала сложим дроби и . Очевидно, знаменатели равны. Согласно соответствующему правилу записываем дробь, числитель которой равен сумме числителей исходных дробей, а знаменатель оставляем прежним, имеем . Сложение выполнено, остается упростить полученную дробь: . Итак, .

Можно было решение вести по-другому: сначала осуществить переход к обыкновенным дробям, после чего провести сложение. При таком подходе имеем .

Теперь вычтем из дроби дробь . Знаменатели дробей равны, поэтому, действуем по правилу вычитания дробей с одинаковыми знаменателями:

Переходим к примерам сложения и вычитания дробей с разными знаменателями. Здесь главная сложность заключается в приведении дробей к общему знаменателю. Для дробей общего вида это довольно обширная тема, ее мы разберем детально в отдельной статье приведение дробей к общему знаменателю . Сейчас же ограничимся парой общих рекомендаций, так как в данный момент нас больше интересует техника выполнения действий с дробями.

Вообще, процесс схож с приведением к общему знаменателю обыкновенных дробей. То есть, знаменатели представляются в виде произведений, дальше берутся все множители из знаменателя первой дроби и к ним добавляются недостающие множители из знаменателя второй дроби.

Когда знаменатели складываемых или вычитаемых дробей не имеют общих множителей, то в качестве общего знаменателя логично взять их произведение. Приведем пример.

Допустим, нам нужно выполнить сложение дробей и 1/2 . Здесь в качестве общего знаменателя логично взять произведение знаменателей исходных дробей, то есть, . В этом случае дополнительным множителем для первой дроби будет 2 . После умножения на него числителя и знаменателя дробь примет вид . А для второй дроби дополнительным множителем является выражение . С его помощью дробь 1/2 приводится к виду . Остается сложить полученные дроби с одинаковыми знаменателями. Вот краткая запись всего решения:

В случае дробей общего вида речь уже не идет о наименьшем общем знаменателе, к которому обычно приводятся обыкновенные дроби. Хотя в этом вопросе все же желательно стремиться к некоторому минимализму. Этим мы хотим сказать, что не стоит в качестве общего знаменателя сразу брать произведение знаменателей исходных дробей. Например, совсем не обязательно брать общим знаменателем дробей и произведение . Здесь в качестве общего знаменателя можно взять .

Переходим к примерам умножения дробей общего вида. Умножим дроби и . Правило выполнения этого действия нам предписывает записать дробь, числитель которой есть произведение числителей исходных дробей, а знаменатель – произведение знаменателей. Имеем . Здесь, как и во многих других случаях при умножении дробей, можно сократить дробь: .

Правило деления дробей позволяет от деления переходить к умножению на обратную дробь. Здесь нужно помнить, что для того, чтобы получить дробь, обратную данной, нужно переставить местами числитель и знаменатель данной дроби. Вот пример перехода от деления числовых дробей общего вида к умножению: . Остается выполнить умножение и упростить полученную в результате дробь (при необходимости смотрите преобразование иррациональных выражений):

Завершая информацию этого пункта, напомним, что любое число или числовое выражение можно представить в виде дроби со знаменателем 1 , поэтому, сложение, вычитание, умножение и деление числа и дроби можно рассматривать как выполнение соответствующего действия с дробями, одна из которых имеет единицу в знаменателе. Например, заменив в выражении корень из трех дробью , мы от умножения дроби на число перейдем к умножению двух дробей: .

Выполнение действий с дробями, содержащими переменные

Правила из первой части текущей статьи применяются и для выполнения действий с дробями, которые содержат переменные. Обоснуем первое из них – правило сложения и вычитания дробей с одинаковыми знаменателями, остальные доказываются абсолютно аналогично.

Докажем, что для любых выражений A , C и D (D тождественно не равно нулю) имеет место равенство на его области допустимых значений переменных.

Возьмем некоторый набор переменных из ОДЗ. Пусть при этих значениях переменных выражения A , C и D принимают значения a 0 , c 0 и d 0 . Тогда подстановка значений переменных из выбранного набора в выражение обращает его в сумму (разность) числовых дробей с одинаковыми знаменателями вида , которая по правилу сложения (вычитания) числовых дробей с одинаковыми знаменателями равна . Но подстановка значений переменных из выбранного набора в выражение обращает его в ту же дробь . Это означает, что для выбранного набора значений переменных из ОДЗ значения выражений и равны. Понятно, что значения указанных выражений будут равны и для любого другого набора значений переменных из ОДЗ, а это означает, что выражения и тождественно равны, то есть, справедливо доказываемое равенство .

Примеры сложения и вычитания дробей с переменными

Когда знаменатели складываемых или вычитаемых дробей одинаковые, то все довольно просто – складываются или вычитаются числители, а знаменатель остается прежним. Понятно, что полученная после этого дробь при надобности и возможности упрощается.

Заметим, что иногда знаменатели дробей отличаются лишь с первого взгляда, но по факту являются тождественно равными выражениями, как например, и , или и . А иногда достаточно упростить исходные дроби, чтобы «проявились» их одинаковые знаменатели.

Пример.

, б) , в) .

Решение.

а) Нам нужно выполнить вычитание дробей с одинаковыми знаменателями. Согласно соответствующему правилу знаменатель оставляем прежним и вычитаем числители, имеем . Действие проведено. Но еще можно раскрыть скобки в числителе и привести подобные слагаемые : .

б) Очевидно, знаменатели складываемых дробей одинаковые. Поэтому, складываем числители, а знаменатель оставляем прежним: . Сложение выполнено. Но несложно заметить, что полученную дробь можно сократить. Действительно, числитель полученной дроби можно свернуть по формуле квадрат суммы как (lgx+2) 2 (смотрите формулы сокращенного умножения), таким образом, имеют место следующие преобразования: .

в) Дроби в сумме имеют разные знаменатели. Но, преобразовав одну из дробей, можно перейти к сложению дробей с одинаковыми знаменателями. Покажем два варианта решения.

Первый способ. Знаменатель первой дроби можно разложить на множители, воспользовавшись формулой разность квадратов, после чего сократить эту дробь: . Таким образом, . Еще не помешает освободиться от иррациональности в знаменателе дроби: .

Второй способ. Умножение числителя и знаменателя второй дроби на (это выражение не обращается в нуль ни при каких значениях переменной x из ОДЗ для исходного выражения) позволяет достичь сразу двух целей: освободиться от иррациональности и перейти к сложению дробей с одинаковыми знаменателями. Имеем

Ответ:

а) , б) , в) .

Последний пример подвел нас к вопросу приведения дробей к общему знаменателю. Там мы почти случайно пришли к одинаковым знаменателям, упрощая одну из складываемых дробей. Но в большинстве случаев при сложении и вычитании дробей с разными знаменателями приходится целенаправленно приводить дроби к общему знаменателю. Для этого обычно знаменатели дробей представляются в виде произведений, берутся все множители из знаменателя первой дроби и к ним добавляются недостающие множители из знаменателя второй дроби.

Пример.

Выполнить действия с дробями: а) , б) , в) .

Решение.

а) Здесь нет надобности что-либо делать со знаменателями дробей. В качестве общего знаменателя берем произведение . В этом случае дополнительным множителем для первой дроби выступает выражение , а для второй дроби – число 3 . Эти дополнительные множители приводят дроби к общему знаменателю, что в дальнейшем позволяет выполнить нужное нам действие, имеем

б) В этом примере знаменатели уже представлены в виде произведений, и никаких дополнительных преобразований не требуют. Очевидно, множители в знаменателях отличаются лишь показателями степеней, поэтому, в качестве общего знаменателя берем произведение множителей с наибольшими показателями, то есть, . Тогда дополнительным множителем для первой дроби будет x 4 , а для второй – ln(x+1) . Теперь мы готовы выполнить вычитание дробей:

в) А в данном случае для начала поработаем со знаменателями дробей. Формулы разность квадратов и квадрат суммы позволяют от исходной суммы перейти к выражению . Теперь понятно, что эти дроби можно привести к общему знаменателю . При таком подходе решение будет иметь следующий вид:

Ответ:

а)

б)

в)

Примеры умножения дробей с переменными

Умножение дробей дает дробь, числитель которой есть произведение числителей исходных дробей, а знаменатель – произведение знаменателей. Здесь, как видите, все привычно и просто, и можно лишь добавить, что полученная в результате выполнения этого действия дробь часто оказывается сократимой. В этих случаях ее сокращают, если, конечно, это необходимо и оправданно.

1. Чтобы сложить дроби с одинаковыми знаменателями, надо сложить их числители, а знаменатель оставить тот же.
2. Чтобы выполнить вычитание дробей с одинаковыми знаменателями, надо из числителя уменьшаемого отнять числитель вычитаемого, а знаменатель оставить тот же.
3. Чтобы сложить или вычесть дроби с разными знаменателями, надо сначала привести их к общему знаменателю, а потом применить правило сложения дробей с общим знаменателем.
4. Произведением дробей является дробь, числитель которой равен произведению числителей этих дробей, а знаменатель - произведением знаменателей этих дробей.
5. Чтобы выполнить деление дроби на дробь, надо делимое умножить на дробь, обратную делителю.
6. Любое натуральное число можно представить в виде дроби с любым натуральным знаменателем.
7. Чтобы привести дробь (или натуральное число) к новому знаменателю, надо воспользоваться основным свойством дроби :

Если числитель и знаменатель дроби умножить или разделить на одно и то же число, не равное нулю, то получится дробь, равная данной.

Правила действий со смешанными числами.

Смешанное число - это сумма натурального числа и правильной дроби. Натуральное число называется целой частью, а правильная дробь - дробной частью смешанного числа.

Например, - смешанная дробь.

1. Чтобы сложить смешанные числа, надо сложить отдельно целые части и отдельно дробные части и полученные результаты сложить. Если в результате сложения дробная часть станет неправильной дробью, то из нее надо выделить целую часть и прибавить к целой части результата.
2. Если дробные части смешанных чисел имеют разные знаменатели, то их сначала надо привести к общему знаменателю, а потом применить правило сложения смешанных чисел.
3. Чтобы выполнить вычитание смешанных чисел, надо вычитание целых и дробных частей выполнить отдельно, а потом результаты сложить. Это выполнимо, если целая и дробная части уменьшаемого соответственно больше целой и дробной части вычитаемого.
4. Если дробная часть уменьшаемого меньше дробной части вычитаемого, то у целой части уменьшаемого надо занять единицу, представить ее в виде дроби с тем же знаменателем и добавить ее к дробной части уменьшаемого. Затем применить правило вычитания дробей.
5. Внимание! Не надо представлять уменьшаемое и вычитаемое целиком в виде неправильной дроби! Это может привести к вычислительным ошибкам!
6. Если смешанные числа имеют разные знаменатели, то перед вычитанием надо привести их к общему знаменателю, а потом применить правило вычитания смешанных чисел.
7. Чтобы умножить или разделить смешанные числа, можно представить их в виде неправильных дробей, а затем применить правило умножения или деления обыкновенных дробей.

Расширение дроби. Сокращение дроби. Сравнение дробей.

Приведение к общему знаменателю. Сложение и вычитание дробей.

Умножение дробей. Деление дробей.

Расширение дроби. Значение дроби не меняется, если умножить её числитель и знаменатель на одно и то же число, отличное от нуля расширением дроби . Например,

Сокращение дроби. Значение дроби не меняется, если разделить её числитель и знаменатель на одно и то же число, отличное от нуля . Это преобразование называется сокращением дроби . Например,

Сравнение дробей. Из двух дробей с одинаковыми числителями та больше, знаменатель которой меньше:

Из двух дробей с одинаковыми знаменателями та больше, числитель которой больше:

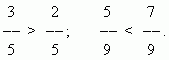
Для сравнения дробей, у которых числители и знаменатели различны, необходимо расширить их, чтобы привести к общему знаменателю.

П р и м е р. Сравнить две дроби:

Использованное здесь преобразование называется приведением дробей к общему знаменателю .

Сложение и вычитание дробей. Если знаменатели дробей одинаковы, то для того, чтобы сложить дроби, надо сложить их числители, а для того, чтобы вычесть дроби, надо вычесть их числители (в том же порядке). Полученная сумма или разность будет числителем результата; знаменатель останется тем же. Если знаменатели дробей различны, необходимо сначала привести дроби к общему знаменателю. При сложении смешанных чисел их целые и дробные части складываются отдельно. При вычитании смешанных чисел мы рекомендуем сначала преобразовать их к виду неправильных дробей, затем вычесть из одной другую, а после этого вновь привести результат, если требуется, к виду смешанного числа.

П р и м е р .

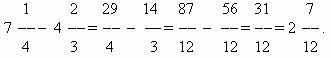
Умножение дробей. Умножить некоторое число на дробь означает умножить его на числитель и разделить произведение на знаменатель. Следовательно, мы имеем общее правило умножения дробей: для перемножения дробей необходимо перемножить отдельно их числители и знаменатели и разделить первое произведение на второе .