Владимир 2002 год
Владимирский государственный университет, Кафедра общей и прикладной физики
Вступление
Символ интеграла введен с 1675г., а вопросами интегрального исчисления занимаются с 1696г. Хотя интеграл изучают, в основном, ученые–математики, но и физики внесли свой вклад в эту науку. Практически ни одна формула физики не обходится без дифференциального и интегрального исчислений. Поэтому, я и решила исследовать интеграл и его применение.
История интегрального исчисления
История понятия интеграла тесно связана с задачами нахождения квадратур. Задачами о квадратуре той или иной плоской фигуры математики Древней Греции и Рима называли задачи на вычисление площадей. Латинское слово quadratura переводится как “придание квадратной формы”. Необходимость в специальном термине объясняется тем, что в античнoe время (и позднее, вплоть до XVIII столетия) еще не были достаточно развиты представления о действительных числах. Математики оперировали с их геометрическими аналогами или скалярными величинами, которые нельзя перемножать. Поэтому и задачи на нахождение площадей приходилось формулировать, например, так: «Построить квадрат, равновеликий данному кругу». (Эта классическая задача “о квадратуре круга” круга» не может, как известно, быть решена с помощью циркуля и линейки.)
Символ ò введен Лейбницем (1675 г.). Этот знак является изменением латинской буквы S (первой буквы слова summ a). Само слово интеграл придумал Я. Б е р у л л и (1690 г.) Вероятн о, оно происходит от латинского integro , которое переводится как приводи ь в прежнее состояние, восстанавливать. (Действительно, операция интегрирования восстанавливает функцию, дифференцированием которой получена подынтегральная функция.) Возможно, происхождение термина инт грал иное: слово integer означает целый.
В современной литературе множество всех первообразных для функции f(х) называется также неопределенным интегралом. Это понятие выделил Лейбниц, который заметил, что в е первообразные функции отличаются на произвольн ю постоянн ю. b
называют определенным интегралом (обо начение ввел К. Фурье (1768-1830), но пределы интегрирования указывал уже Эй лер).
Многие значительные достижения математиков Древней Греции в решении задач на нахождение квадратур (т. е. вычисление площадей) плоских фигур, а также кубатур (вычисление объемов) тел связаны с применением метода исчерпывания, предложенным Евдоксом Книдским (ок. 408 - ок. 355 до н.э.). С помощью этого метода Евдокс доказал, например, что площади двух кругов относятся как квадраты их диаметров, а объем конуса равен 1/3 объёма цилиндра, имеющего такие же основание и высоту.
Метод Евдокса был усовершенствован Архимедом. Основные этапы, характеризующие метод Архимеда: 1) доказывается, что площадь круга меньше площади любого описанного около него правильного многоугольника, но больше площади любого вписанного; 2) доказывается, что при неограниченном удвоении числа сторон разность площадей этих многоугольн иков стремится к нулю; 3) для вычисления площади круга остается найти значение, к которому стремится отношение площади правильного многоугольника при неограниченном удвоении числа его сторон.
С помощью метода исчерпывания, целого ряда других остроумных соображений (в том числе с привлечением моделей механики) Архимед решил многие задачи. Он дал оценку числа p (3.10/71 Архимед предвосхитил многие идеи интегрального исчисления. (Добавим, что практически и первые теоремы о пределах были доказаны им.) Но потребовалось более полутора тысяч лет, прежде чем эти идеи нашли четкое выражение и были доведены до уровня исчисления. Математики XVII столетия, получившие многие новые результаты, учились на трудах Архимеда. Активно применялся и другой метод - метод неделимых, который также зародился в Древней Греции (он связан в первую очередь с атомистическими воззрениями Демокрита). Например, криволинейную трапецию
(рис. 1, а) они представляли себе составленной из вертика
ьных отрезков длиной f(х), которым тем не менее приписывали
площадь, равн
ю бесконечно малой величине f(х)
. В соответствии с таким пониманием искомая площадь считалась равной сумме бесконечно большого числа бесконечно малых площадей. Иногда даже подчеркивалось, что отдельные слагаемые в этой сумме - нули, но нули особого рода, которые, сложенные в бесконечном числе, дают вполне определенную положительную сумму. На такой кажущейся теперь по меньшей мере сомнительной
основе И. Кеплер (1571-1630) в своих сочинениях “Новая астрономия”. (1609 г.) и «Стереометрия винных бочек» (1615 г.) правильно вычислил ряд площадей (например, площадь фигуры ограниченной эллипсом) и объемов (тело разрезалось на 6ecконечно тонкие пластинки). Эти исследования были продолжены итальянскими математиками Б. Кавальери (1598-1647) и Э.Торричелли (1608-1647). Сохраняет свое значение и в наше время сформулированный Б. Кавальери принцип, введенный им при некоторых дополнительных предположениях. Пусть требуется найти площадь фигуры, изображенной на рисунке 1,б, где кривые, ограничивающие фигуру сверху и снизу, имеют уравнения y = f(x) и y=f(x)+c. Представляя фигуру составленной из «неделимых», по терминологии Кавальери, бесконечно тонких столбиков, замечаем, что все они имеют общую длину с. Передвигая их в вертикальном направлении, можем составить из них прямоугольник с основанием b-а и высотой с. Поэтому искомая площадь равна площади полученного прямоугольника, т.е. S = S1 = c (b – а). Общий принцип Кавальери для площадей плоских фигур формулируется так: Пусть прямые некоторого пучка параллельных пересекают фигуры Ф1 и Ф2 по отрезкам равной длины (рис. 1,в). Тогда площади фигур Ф1 и Ф2 равны. Аналогичный принцип действует в стереометрии и оказывается полезн
м при нахождении объемов. В XVII в. были сделаны многие открытия, относящиеся к интегральному исчислению. Так, П.Ферма уже в 1629 г. задачу квадратуры любой кривой у = хn, где п - целое (т.е по существу вывел формулу ò хndx = (1/n+1)хn+1), и на этой основе решил ряд задач на нахождение центров тяжести. И. Кеплер при выводе своих знаменитых законов движения планет фактически опирался на идею приближенного интегрирования. И. Барроу (1630-1677), учитель Ньютона, близко подошел к пониманию связи интегрирования и дифференцирования. Большое значение имели работы по представлению функций в виде степенных рядов. Однако при всей значимости результатов, полученных многими чрезвычайно изобретательными математиками XVII столетия исчисления еще не было. Необходимо было выделить общие идеи лежащие в основе решения многих частных задач, а также установить связь операций дифференцирования и интегрирования, дающую достаточно общий алгоритм. Это сделали Ньютон и Лейбниц, открывшие независимо друг от друга факт, известным под названием формулы Ньютона - Лейбница. Тем самым окончательно оформился общий метод. Предстояло еще научится находить первообразные многих функций, дать логические нового исчисления и т. п. Но главное уже было сделано: дифференциальное и интегральное исчисление создано. Методы математического анализа активно развивались в следующем столетии (в первую очередь следует назвать имена Л. Эйлера, завершившего систематическое исследование интегрирования элементарных функций, и И. Бернулли). В развитии интегрального исчисления приняли участие русские математики М.В.Остроградский (1801-1862), В.Я.Буняковский (1804-1889), П.Л.Ч
бышев (1821-1894). Принципиальное значение имели, в частности, результаты Чебышева, доказавшего, что существуют интегралы, не выразимые через элементарные функции. Строгое изложение теории интеграла появилось только в прошлом веке. Решение этой задачи связано с именами О.Коши, одного из крупнейших математиков, немецкого ученого Б.Римана (1826-1866), французского математика Г.Дарбу (1842-1917). Ответы на многие вопросы, связанные с существованием площадей и объемов фигур, были получены с созданием К. Жорданом (1838-1922) теории меры. План
1. История интегрального исчисления. 2. Определение и свойства интеграла. 3. Криволинейная трапеция. 4. Свойства определенного интеграла. 5. Набор стандартных картинок. 6. Применение интеграла. История интегрального исчисления
История понятия интеграла тесно связана с задачами нахождения квадратур. Задачами о квадратуре той или иной плоской фигуры математики Древней Греции и Рима называли задачи на вычисление площадей. Латинское слово quadratura переводится как “придание квадратной формы”. Необходимость в специальном термине объясняется тем, что в античнoe время (и позднее, вплоть до XVIII столетия) еще не были достаточно развиты представления о действительных числах. Математики оперировали с их геометрическими аналогами или скалярными величинами, которые нельзя перемножать. Поэтому и задачи на нахождение площадей приходилось формулировать, например, так: «Построить квадрат, равновеликий данному кругу». (Эта классическая задача “о квадратуре круга” круга» не может, как известно, быть решена с помощью циркуля и линейки.) Символ ò введен Лейбницем (1675 г.). Этот знак является изменением латинской буквы S (первой буквы слова summa). Само слово интеграл придумал Я. Б е р н у л л и (1690 г.). Вероятно, оно происходит от латинского integro, которое переводится как приводить в прежнее состояние, восстанавливать. (Действительно, операция интегрирования «восстанавливает» функцию, дифференцированием которой получена подынтегральная функция.) Возможно, происхождение термина интеграл иное: слово integer означает целый. В ходе переписки И. Бернулли и Г. Лейбниц согласились с предложением Я. Бернулли. Тогда же, в 1696 г., появилось и название новой ветви математики-интегральное исчисление (calculus integralis), которое ввел И. Бернулли. Другие известные ермины, относящиеся к интегральному исчислению, появились заметно позднее. Употребляющееся сейчас название первообразная функция заменило более раннее «примитивная функция», которое ввел Лагранж (1797 г.). Латинское слово primitivus переводится как «начальный»: F(x) = ò f(x)dx - начальная (или первоначальная, или первообразная) для f(x), которая получается из F(x) дифференцированием. В современной литературе множество всех первообразных для функции f(х) называется также неопределенным интегралом. Это понятие выделил Лейбниц, который заметил, что все первообразные функции отличаются на произвольную постоянную. b называют определенным интегралом (обозначение ввел К. Фурье (1768-1830), но пределы интегрирования указывал уже Эйлер). Многие значительные достижения математиков Древней Греции в решении задач на нахождение квадратур (т. е. вычисление площадей) плоских фигур, а также кубатур (вычисление объемов) тел связаны с применением метода исчерпывания, предложенным Евдоксом Книдским (ок. 408 - ок. 355 до н.э.). С помощью этого метода Евдокс доказал, например, что площади двух кругов относятся как квадраты их диаметров, а объем конуса равен 1/3 объёма цилиндра, имеющего такие же основание и высоту. Метод Евдокса был усовершенствован Архимедом. Основные этапы, характеризующие метод Архимеда: 1) доказывается, что площадь круга меньше площади любого описанного около него правильного многоугольника, но больше площади любого вписанного; 2) доказывается, что при неограниченном удвоении числа сторон разность площадей этих многоугольников стремится к нулю; 3) для вычисления площади круга остается найти значение, к которому стремится отношение площади правильного многоугольника при неограниченном удвоении числа его сторон. С помощью метода исчерпывания, целого ряда других остроумных соображений (в том числе с привлечением моделей механики) Архимед решил многие задачи. Он дал оценку числа p (3.10/71 Архимед предвосхитил многие идеи интегрального исчисления. (Добавим, что практически и первые теоремы о пределах были доказаны им.) Но потребовалось более полутора тысяч лет, прежде чем эти идеи нашли четкое выражение и были доведены до уровня исчисления. Математики XVII столетия, получившие многие новые результаты, учились на трудах Архимеда. Активно применялся и другой метод - метод неделимых, который также зародился в Древней Греции (он связан в первую очередь с атомистическими воззрениями Демокрита). Например, криволинейную трапецию (рис. 1, а) они представляли себе составленной из вертикальных отрезков длиной f(х), которым тем не менее приписывали площадь, равную бесконечно малой величине f(х)dx. В соответствии с таким пониманием искомая площадь считалась равной сумме бесконечно большого числа бесконечно малых площадей. Иногда даже подчеркивалось, что отдельные слагаемые в этой сумме - нули, но нули особого рода, которые, сложенные в бесконечном числе, дают вполне определенную положительную сумму. На такой кажущейся теперь по меньшей мере сомнительной основе И. Кеплер (1571-1630) в своих сочинениях “Новая астрономия”. (1609 г.) и «Стереометрия винных бочек» (1615 г.) правильно вычислил ряд площадей (например, площадь фигуры ограниченной эллипсом) и объемов (тело разрезалось на 6ecконечно тонкие пластинки). Эти исследования были продолжены итальянскими математиками Б. Кавальери (1598-1647) и Э.Торричелли (1608-1647). Сохраняет свое значение и в наше время сформулированный Б. Кавальери принцип, введенный им при некоторых дополнительных предположениях. Пусть требуется найти площадь фигуры, изображенной на рисунке 1,б, где кривые, ограничивающие фигуру сверху и снизу, имеют уравнения y = f(x) и y=f(x)+c. Представляя фигуру составленной из «неделимых», по терминологии Кавальери, бесконечно тонких столбиков, замечаем, что все они имеют общую длину с. Передвигая их в вертикальном направлении, можем составить из них прямоугольник с основанием b-а и высотой с. Поэтому искомая площадь равна площади полученного прямоугольника, т.е. S = S1 = c (b – а). Общий принцип Кавальери для площадей плоских фигур формулируется так: Пусть прямые некоторого пучка параллельных пересекают фигуры Ф1 и Ф2 по отрезкам равной длины (рис. 1,в). Тогда площади фигур Ф1 и Ф2 равны. Аналогичный принцип действует в стереометрии и оказывается полезным при нахождении объемов. В XVII в. были сделаны многие открытия, относящиеся к интегральному исчислению. Так, П.Ферма уже в 1629 г. задачу квадратуры любой кривой у = хn, где п - целое (т.е по существу вывел формулу ò хndx = (1/n+1)хn+1), и на этой основе решил ряд задач на нахождение центров тяжести. И. Кеплер при выводе своих знаменитых законов движения планет фактически опирался на идею приближенного интегрирования. И. Барроу (1630-1677), учитель Ньютона, близко подошел к пониманию связи интегрирования и дифференцирования. Большое значение имели работы по представлению функций в виде степенных рядов. Отдел образования гомельского городского Исполнительного комитета Государственное учреждение образования «Гимназия №71 г. Гомеля» Конкурсной работы «Применение дифференциального и интегрального исчисления к решению физических и геометрических задач в MATLab» Исполнитель: Орехова Ксения Ивановна, учащаяся 9Б класса Руководитель: Горский Сергей Михайлович, учитель информатики Государственного учреждения образования «Гимназия №71 г. Гомеля» Введение 1. История интегрального и дифференциального исчисления 2. Дифференциал в физике 3. Приложения определенного интеграла к решению некоторых задач механики и физики 4. Дифференциальные уравнения 5. Примеры решения задач в matlab Список использованных источников Факультативный курс «Применение дифференциального и интегрального исчисления к решению физических и геометрических задач» имеет своей целью изучение курса математического анализа на основе практического освещения материала, на основе использования методов данного раздела математики для решения задач геометрии и физики; а так же реализации этих задач на компьютере (с помощью пакета MATLAB). В результате можно сказать, что такое объёмное, не конкретное формулирование темы и цели факультативного курса даёт возможным его реализацию в школе. В школьном курсе алгебры и начал анализа курс «Применение дифференциального и интегрального исчисления к решению физических и геометрических задач» направлен на изучение определённого интеграла. Место темы в школьном курсе математики
. Факультативный курс «Применение интегрального исчисления к решению физических и геометрических задач» углубляет материал курса алгебры и начал анализа в одиннадцатом классе и раскрывает возможности для практического закрепления материала по темам, входящим в школьный курс математики. Это темы «Производная функции», «Определённый интеграл» в алгебре, и некоторые темы в геометрии и физике. В результате данный факультативный курс реализует межпредметную связь алгебры и математического анализа с геометрией, информатикой и физикой. Развитию у учащихся правильных представлений о характере отражения алгеброй основных элементов в геометрии и физике, роли математического моделирования в научном познании способствует знакомство их с решением и визуализацией различных математических задач на компьютере. Изложение факультативного курса базируется на основных возможностях версии 6.1 пакета математических и инженерных вычислений MATLAB, ставшего в настоящее время стандартным средством поддержки изучения высшей математики, численного анализа и других учебных курсов во многих университетах. Учащимся излагаются основные возможности численных и символьных вычислений, программирования и визуализации результатов, предоставляемые ядром системы MATLAB и его пакета расширения SymbolicMathToolbox. Основные понятия факультативного курса
: определённый интеграл, длина кривой, площадь, поверхность вращения, цилиндрическая поверхность, объём тела и др. Цели факультативного курса.
1. Обучающие
: провести практическое закрепление по теме «Определённый интеграл», познакомить учащихся с пакетом математических и инженерных вычислений MATLAB 6.1, проиллюстрировать реализацию межпредметной связи математического анализа с геометрией, информатикой и физикой. 2. Воспитывающие:
создание условий для успешного профессионального самоопределения учащихся посредством решения трудных задач с использованием компьютера, воспитание мировоззрения и ряда личностных качеств, средствами углубленного изучения математики. 3. Развивающие:
расширение кругозора учащихся, развитие математического мышления, формирование активного познавательного интереса к предмету, развитие профессиональных интересов учащихся, развитие навыков самостоятельной и исследовательской деятельности, развитие рефлексии учащихся (осознание своих склонностей и способностей, необходимыми для будущей профессиональной деятельности). Программа: Построение астроиды t=-2*pi:pi/20:2*pi; h=300; figure("Units","Pixels","position", xlabel("x"); ylabel("y"); axis([-3, 3, -3, 3]); % Поверхность вращения t=-2*pi:pi/20:2*pi; Meshgrid(t,v); set(hFigure,"Color",); set(hAxes,"Color",); xlabel("x"); ylabel("y"); zlabel("z"); hPlot=plot(X,Y); set(hPlot,"LineWidth",5) set(hPlot,"Color",) Задача 5. Построить в полярных координатах лемнискату Бернулли: Программа: for p=0:pi/60:2*pi if 2*a^2*cos(2*p)>=0 set(hFigure,"Color",); hP=polar(phi,r); set(hP,"LineWidth",2); Результат (рис. 17): Задача 6. Используя численные и символьные вычисления в MATLAB найти: а) определённый интеграл; б) двойной интеграл; в) поверхностный интеграл (1-го рода). а) Классической задачей численного анализа является задача о вычислении определённых интегралов. Из всех методов вычисления определённых интегралов самым простым, но в то же время довольно успешно применяемым является метод трапеции. В MATLAB для этого метода предусмотрена функция: trapz(x,y) (команда edit trapz позволяет вывести текст этой функции). Одномерный массив х (вектор) содержит дискретные значения аргументов подынтегральной функции. Значения подынтегральной функции в этих точках сосредоточены в одномерном массиве y. Чаще всего для интегрирования выбирают равномерную сетку, то есть значения элементов массива х отстоят друг от друга на одну и ту же величину – шаг интегрирования. Точность вычисления интеграла зависит от величины шага интегрирования: чем меньше этот шаг, тем больше точность. Задача 7. Вычислить интеграл методом трапеции с различными шагами интегрирования (для наблюдения 14 десятичных цифр после запятой нужно предварительно ввести и исполнить команду formatlong). Программа: Результат: functiont=trap(dx) y=sin(x).*exp(-x); t=trapz(x,y); >> format long ans = 0.42255394026468 >> trap(0.1) ans = 0.50144886299125 >> trap(0.01) ans = 0.50226667654901 >> trap(0.001) ans = 0.50227485744814 Метод трапеций является очень универсальным методом и хорошо подходит интегрирования не слишком гладких функций. Если же функция под знаком интеграла является гладкой (существуют и непрерывны несколько первых производных), то лучше применять методы интегрирования более высоких порядков точности. При одном и том же шаге интегрирования методы более высоких порядков точности достигают более точных результатов. В системе МАТLАВ методы интегрирования более высоких порядков точноcти реализуются функциями quad (метод Симпсона) и quad8 (метод Ньютона-Котеса 8-го порядка точности). Оба этих метода являются к тому же адаптивными
. Последнее означает, что пользователю нет необходимости контролировать достигнутую точность результата путем сравнения последовательных значении, соответствующих разным шагам интегрирования. Все это указанные данные функции выполняют самостоятельно. У функции quad8 более высокий порядок точности по сравнению с функцией quad, что очень хорошо для гладких функций, так как обеспечивается более высокая точность результата при большем шаге интегрирования (меньшем объеме отчислений). Однако функция quad может иметь не меньшее, а даже большее быстродействие для не слишком гладких функций (разрывны или велики по абсолютной величине вторая или третья производные). В любом случае обе эти функции по умолчанию обеспечивают одинаковую относительную точность результата, равную 0.001. Как и многие другие функции системы МАТLАВ, функции quad и quad8 могут принимать различное количество параметров. Минимальный формат вызова этих функций включает в себя три параметра: имя подынтегральной функции, нижний предел интегрирования и верхний предел интегрирования. Если применяется четвертый параметр, то он является требуемой относительной точностью результата вычислений. Кстати, если обе эти адаптивные функции не могут обеспечить получение необходимой точности (расходящийся или близкий к этому интеграл), то они возвращают символическую бесконечность Inf. Для вычисления определённых интегралов символьными методами можно использовать два варианта решения: напрямую или по этапам (с подстановкой символьных чисел). Задача 8. Вычислить определённый интеграл . Программа: Результат: a1=sym("0"); b1=sym("2"); % 1 способ: работа с подстановкой символьных чисел symbol=int(w,"t",a,b) symbol2a=subs(symbol,,) number=vpa(symbol2a) % 2 способ: работа с символьными числами symbol2b=int(w,"t",a1,b1) symbol = 2.6666666666666666667 Задача 9. Вычислить площадь поверхности, полученной вращением астроиды вокруг оси Ox
: Программа: Результат: t1=sym("0"); t2=sym("pi/2"); a=sym("1"); x=a*cos(t)^3; y=a*sin(t)^3; f=y.*sqrt(diff(x)^2+diff(y)^2); symbol=simplify(int(4*pi*f,"t",t1,t2)) number=vpa(symbol) symbol = б) Двойные интегралы сводятся к вычислению повторных определённых интегралов, один из которых является внутренним, а другой внешним. Внутренний интеграл является подынтегральной функцией для внешнего интеграла. Можно было бы для численных вычислений написать некоторую цепочку вычислений, в которой многократные вычисления подынтегральной функции сводились бы к многократным вызовам функции quad. Однако нет необходимости делать это самостоятельно, так как в системе MATLAB для этого имеется специальная функция dblquad. Задача 8. Вычислить интеграл Программа: Результат: function z=fof(x,y) z=x.*sin(y)+y.*sin(x); >> format long >> dblquad("fof",0,1,1,2) 1.16777110966887 Задача 9. С помощью символьных вычислений получить следующие интегралы Программа: z=sym("x*sin(y)+y*sin(x)"); i2=int(z,"x",0,1) i3=int(int(z,"x"),"y") i4=int(int(z,"x",1,2),"y",0,1) i5=int(int(x+y,"y",x,1),"x",0,1) i1 = 1/2*x^2*sin(y)-y*cos(x) 1/2*sin(y)-y*cos(1)+y 1/2*x^2*cos(y)-1/2*y^2*cos(x) 1/2*cos(2)-cos(1)+3/2 Так как символьные вычисления не дают погрешности метода вычисления и сами по себе они более точные, то можно увидеть, что функция dblquad даёт точный результат до 7 знака после запятой. в) Из высшей математики известно, что к определенным и двойным интегралам могут быть сведены многие другие типы интегралов, например поверхностный интеграл 1-го рода. Так как при его нахождении используется дифференцирование под знаком интеграла, то использовать численные вычисления некорректно. Задача 10. Вычислить поверхностный интеграл 1-го рода: , где S
– часть плоскости , лежащая в первом октанте (по теореме 2). Программа: Результат: fun=subs(f2,z,f1) d=1+diff(f1,x)^2+diff(f1,y)^2 syms x1 x2 y1 y2 intpov1=int(int(fun*sqrt(d),"y",y1,y2),"x",x1,x2) number=vpa(intpov1) fun = Задача 11. Вычислить поверхностный интеграл 1-го рода Сначала создадим функцию, описывающую поверхность по которой происходит интегрирование: function =pov; syms x y z u v a x=a*sin(u)*cos(v); y=a*sin(u)*sin(v); Программа: syms x y z u v a f=sym("x^2+y^2"); E=diff(x0,"u")^2+diff(y0,"u")^2+diff(z0,"u")^2; G=diff(x0,"v")^2+diff(y0,"v")^2+diff(z0,"v")^2; F=diff(x0,"u")*diff(x0,"v")+diff(y0,"u")* diff(y0,"v")+diff(z0,"u")*diff(z0,"v"); W=sqrt(E*G-F^2); f2=W*subs(f,,); syms u1 u2 v1 v2 intpov=p*int(int(f2,"v",v1,v2),"u",u1,u2) intpov2=simplify(intpov) number=vpa(intpov2) int=subs(intpov2,a,b) intpov = 4/3*a^2*pi*(a^4)^(1/2)*4^(1/2) 8/3*a^4*pi*csgn(a^2) 8.377580412*a^4*csgn(a^2) Примечание. Функция сsgn является специфической в MATLAB. Она не может быть введена пользователем и возникает только при оперировании с функцией simplify (упрощение символьных выражений). Например: >> syms a t >> t=csgn(a^2)*a^2 Undefined function or variable "csgn". >> simplify((a^4)^(1/2)) >> simplify((a^8)^(1/4)) >> simplify((a^9)^(1/3)) 1. Ануфриев, И.Е. Самоучитель MatLab 5.3/6.х / И.Е. Ануфриев. - СПб.: БХВ-Петербург, 2002. - 736 с. 2. Берман, Г.Н. Сборник задач по курсу математического анализа / Г.Н. Берман, И.Г. Араманович, А.Ф. Бермант и др. - М.: Наука, 1966. - 456 с. 3. Бермант, А.Ф. Краткий курс математического анализа для втузов / А.Ф. Бермант, И.Г. Араманович. - М.: Наука, 1966. - 736 с. 4. Гультяев, А. Визуальное моделирование в среде MatLab / А. Гультяев. - СПб.: Питер, 2001. - 553 с. 5. Демидович, Б.П. Задачи и упражнения по математическому анализу для втузов / Б.П. Демидович, Г.С. Бараненков, В.А. Ефименко и др. - М.: Наука, 1966. - 472 с. 6. Лазарев, Ю.Ф. MatLab 5.х / Ю.Ф. Лазарев. - Киев: BHV, 2000. - 388 с. 7. Мартынов, Н.Н. Matlab 5.х: вычисления, визуализация, программирование / Н.Н. Мартынов, А.П. Иванов. - М.: КУДИЦ-ОБРАЗ, 2000. - 336 с. 8. Куринной, Г.Ч. Математика: Справочник / Г.Ч. Куринной. - Харьков: Фолио; Ростов на Дону: Феникс, 1997. - 463 с. 9. Пискунов, Н.С. Дифференциальное и интегральное исчисление для втузов в 2 томах / Н.С. Пискунов. - М.: Наука, 1966. - 2 т. - 312 с. 10. Фихтенгольц, Г.М. Курс дифференциального и интегрального исчисления в 3 томах / Г.М. Фихтенгольц. - М.: Государственное изд-во физико-математической литературы, 1959. - т. 1-3. 11. Сайты http://www/informika.ru, htt://www.softline.ru, http://matlab.ru. Интегральное
исчисление – это раздел математического анализа, в котором изучаются интегралы,
их свойства, способы вычисления и приложения. Вместе с дифференциальным
исчислением оно составляет основу аппарата математического анализа. Даты возникновения некоторых
математических знаков Значение Когда знак введен, год Знаки объектов бесконечность Дж. Валлис отношение длины окружности к
диаметру корень квадратный из неизвестные или переменные
величины Р. Декарт Знаки операций сложение немецкие математики конец XV в. вычитание умножение У. Оутред умножение Г. Лейбниц Г. Лейбниц Р. Декарт X. Рудольф логарифм И. Кеплер Б. Кавальери арксинус Ж. Лагранж дифференциал Г. Лейбниц интеграл Г. Лейбниц производная Г. Лейбниц определенный интеграл факториал У. Гамильтон многие математики И. Бернулли Знаки отношений равенство Р. Рекорд Т. Гарриот сравнимость параллельность У. Оутред перпендикулярность П. Эригон Интегральное
исчисление возникло из рассмотрения большого числа задач естествознания и
математики. Важнейшие из них – физическая задача определения пройденного за
данное время пути по известной, но, быть может, переменной скорости движения и
значительно более древняя задача вычисления площадей и объемов геометрических
фигур (см. Геометрические задачи на экстремум). Центральным
в интегральном исчислении является понятие интеграла, которое, однако, имеет
две различные трактовки, приводящие соответственно к понятиям неопределенного и
определенного интегралов. В
дифференциальном исчислении была введена операция дифференцирования функций.
Рассматриваемая в интегральном исчислении обратная к дифференцированию
математическая операция называется интегрированием или, точнее, неопределенным
интегрированием. В
чем же состоит эта обратная операция и в чем ее неопределенность? Операция
дифференцирования сопоставляет заданной функции ее производную . Допустим, что мы хотим,
исходя из заданной функции , найти такую функцию , производной
которой является функция , т. е. . Такая функция называется первообразной
функции . Значит,
обратная дифференцированию операция – неопределенное интегрирование – состоит в
отыскании первообразной данной функции. Заметим,
что, наряду с функцией , первообразной для функции , очевидно, будет
также любая функция Таким
образом, в отличие от дифференцирования, сопоставлявшего функции единственную
другую функцию – производную первой, неопределенное интегрирование приводит не
к одной конкретной функции, а к целому набору функций, и в этом его
неопределенность. Однако
степень этой неопределенности не так уж велика. Напомним, что если производная
некоторой функции равна нулю во всех точках какого-то промежутка, то это
функция, постоянная на рассматриваемом промежутке (на промежутках, где скорость
изменения переменной величины везде равна нулю, она не меняется). Значит, если на каком-то
промежутке ,
то функция постоянна
на этом промежутке, поскольку ее производная равна нулю во всех точках промежутка. Итак,
две первообразные одной и той же функции могут отличаться на промежутке только
постоянным слагаемым. Первообразные
функции обозначают
символом где
знак читается:
интеграл. Это так называемый неопределенный интеграл. По доказанному,
неопределенный интеграл изображает на рассматриваемом промежутке не одну
конкретную функцию, а любую функцию вида где
- какая-то
первообразная функции на данном промежутке, а - произвольная
постоянная. Например,
на всей числовой оси Мы
здесь специально обозначили аргументы подынтегральных функций различными
символами: ,
чтобы обратить внимание на независимость первообразной как функции от выбора
буквы, используемой для обозначения ее аргумента. Проверка
написанных равенств выполняется простым дифференцированием их правых частей, в
результате которого получаются стоящие в левых частях под знаком интеграла
функции ,
, соответственно. Полезно
иметь в виду также следующие очевидные соотношения, непосредственно вытекающие
из определений первообразной, производной, дифференциала и из соотношения (1)
для неопределенного интеграла: Отыскание
первообразной часто облегчают некоторые общие свойства неопределенного
интеграла: (вынесение
постоянного множителя); (интегрирование
суммы); если (замена
переменной). Эти
соотношения также проверяются непосредственно с использованием соответствующих
правил дифференцирования. Найдем
закон движения свободно падающего в пустоте тела, исходя из единственного
факта, что при отсутствии воздуха ускорение свободного падения вблизи поверхности
Земли постоянно и не зависит от особенностей падающего тела. Фиксируем
вертикальную координатную ось; направление на оси выберем в сторону к Земле.
Пусть -
координата нашего тела в момент . Нам известно, таким образом, что и - постоянная.
Требуется найти функцию - закон движения. Поскольку
, где , то,
последовательно интегрируя, находим Итак,
мы нашли, что где
и - какие-то
постоянные. Но падающее тело подчиняется все-таки одному конкретному закону
движения, в котором уже нет никакого произвола. Значит, есть еще какие-то
условия, которые мы пока не использовали; они позволяют среди всех
«конкурирующих» законов (3) выбрать тот, который соответствует конкретному
движению. Эти условия легко указать, если разобраться в физическом смысле
постоянных и
. Если
сравнить крайние члены соотношения (2) при , то выяснится, что , а из (3) при получается, что . Таким образом,
математика сама напомнила нам, что искомый закон движения вполне
определится, если указать начальное положение и начальную скорость тела. В частности,
если и , получаем . Отметим
теперь, что между операцией нахождения производной (дифференцированием) и
операцией отыскания первообразной (неопределенным интегрированием) имеется,
кроме указанного выше, еще целый ряд принципиальных отличий. В частности,
следует иметь в виду, что если производная любой комбинации элементарных
функций сама выражается через элементарные функции, т.е. является элементарной
функцией, то первообразная элементарной функции уже не всегда является функцией
элементарной. Например, первообразная элементарной
функции (называемая
интегральным синусом и обозначаемая специальным символом ), как можно доказать, не
выражается в элементарных функциях. Таким образом, принципиальный
математический вопрос о существовании первообразной у наперед заданной функции
не надо смешивать с не всегда разрешимой задачей об отыскании этой
первообразной среди элементарных функций. Интегрирование часто является
источником введения важных и широко используемых специальных функций, которые
изучены ничуть не хуже таких «школьных» функций, как или , хотя и не входят в список
элементарных функций. Наконец,
отметим, что отыскание первообразной, даже когда она выражается в элементарных
функциях, скорее напоминает искусство, чем канонический алгоритм вычислений,
подобный алгоритму дифференцирования. По этой причине найденные первообразные
наиболее часто встречающихся функций собраны в виде справочных таблиц
неопределенных интегралов. Следующая микротаблица такого рода, очевидно,
равносильна микротаблице производных соответствующих основных элементарных
функций: Мы,
пока говорили об обращении операции дифференцирования, пришли в этой связи к
понятиям первообразной, неопределенного интеграла и дали первоначальное
определение этих понятий. Теперь
укажем иной, куда более древний подход к интегралу, который послужил основным
первоначальным источником интегрального исчисления и привел к понятию
определенного интеграла или интеграла в собственном смысле этого слова. Этот
подход четко прослеживается уже у древнегреческого математика и астронома Евдокса
Книдского (примерно 408-355 до н.э.) и Архимеда, т.е. он возник задолго до
появления дифференциального исчисления и операции дифференцирования. Вопрос,
который рассматривали Евдокс и Архимед, создав при его решении «метод
исчерпывания», предвосхитивший понятие интеграла – это вопрос о вычислении
площади криволинейной фигуры. Ниже мы рассмотрим этот вопрос, а пока поставим,
вслед за И. Ньютоном, следующую задачу: по известной в любой момент из промежутка
времени скорости
тела
найти величину перемещения тела за этот промежуток времени. Если
бы был известен закон движения, т.е. зависимость координаты тела от времени, то
ответ, очевидно, выражался бы разностью . Более того, если бы мы знали
какую-либо первообразную функции на промежутке , то, поскольку , где - постоянная,
можно было бы найти искомую величину перемещения в виде разности , которая совпадает
с разностью .
Это очень полезное наблюдение, однако если первообразную данной функции указать не
удается, то действовать приходится совсем иначе. Будем
рассуждать следующим образом. Если
промежуток отдельными
моментами ,
такими, что ,
разбить на очень мелкие временные промежутки , , то на каждом из этих коротких
промежутков скорость тела не успевает заметно измениться.
Фиксировав произвольно момент , можно таким образом приближенно
считать, что на промежутке времени движение происходит с постоянной
скоростью .
В таком случае для величины пути, пройденного за промежуток времени , получаем
приближенное значение , где . Складывая эти величины, получаем
приближенное значение для
всего перемещения на промежутке . Найденное
приближенное значение тем точнее, чем более мелкое разбиение промежутка мы произведем,
т.е. чем меньше будет величина наибольшего из промежутков , на которые разбит
промежуток . Значит,
искомая нами величина перемещения есть предел сумм
вида (4), когда величина стремится к нулю. Суммы
специального вида (4) называются интегральными суммами для функции на промежутке , а их предел (5),
получаемый при неограниченном мельчании разбиений, называется интегралом (или
определенным интегралом) от функции на промежутке . Интеграл обозначается
символом в
котором числа называются
пределами интегрирования, причем - нижним, a - верхним пределом
интегрирования; функция , стоящая под знаком интеграла,
называется подынтегральной функцией; - подынтегральным выражением; - переменной
интегрирования. Итак,
по определению, Значит,
искомая величина перемещения тела за временной промежуток при известной скорости движения
выражается интегралом (6) от функции по промежутку . Сопоставляя
этот результат с тем, который на языке первообразной был указан в начале
рассмотрения этого примера, приходим к знаменитому соотношению: если
. Равенство
(7) называется формулой Ньютона-Лейбница. В левой его части стоит понимаемый
как предел (6) интеграл, а в правой – разность значений (в концах и промежутка
интегрирования) функции , первообразной подынтегральной
функции .
Таким образом, формула Ньютона-Лейбница связывает интеграл (6) и первообразную.
Этой формулой можно, следовательно, пользоваться в двух противоположных
направлениях: вычислять интеграл, найдя первообразную, или получать приращение
первообразной, найдя из соотношения (6) интеграл. Мы увидим ниже, что оба эти
направления использования формулы Ньютона-Лейбница весьма важны. Интеграл
(6) и формула (7) в принципе решают поставленную в нашем примере задачу. Так,
если (как
это имеет место в случае свободного падения, начинающегося из состояния покоя,
т.е. с ),
то, найдя первообразную перемещения
за время, прошедшее от момента до момента . На
основе разобранной только что физической задачи, приведшей нас к интегралу и
формуле Ньютона-Лейбница, обобщая сделанные наблюдения, можно теперь сказать,
что если на некотором промежутке задана функция , то, разбивая промежуток точками , составляя
интегральные суммы где
, , и переходя к
пределу при ,
где , мы
получаем по определению интеграл от
функции по
промежутку .
Если при этом на
, т.е. - первообразная
функции на
промежутке ,
то имеет место формула Ньютона-Лейбница: ЛЕОНАРД ЭЙЛЕР
Эйлер,
крупнейший математик XVIII в., родился в Швейцарии. В 1727 г. по приглашению
Петербургской академии наук он приехал в Россию. В Петербурге Эйлер попал в
круг выдающихся ученых: математиков, физиков, астрономов, получил большие
возможности для создания и издания своих трудов. Он работал с увлечением и
вскоре стал, по единодушному признанию современников, первым математиком
мира. Научное
наследие Эйлера поражает своим объемом и разносторонностью. В списке его
трудов более 800 названий. Полное собрание сочинений ученого занимает 72
тома. Среди его работ – первые учебники по дифференциальному и интегральному
исчислению. В
теории чисел Эйлер продолжил деятельность французского математика П. Ферма и
доказал ряд утверждений: малую теорему Ферма, великую теорему Ферма для
показателей 3 и 4 (см. Ферма великая теорема). Он сформулировал проблемы,
которые определили горизонты теории чисел на десятилетия. Эйлер
предложил применить в теории чисел средства математического анализа и сделал
первые шаги по этому пути. Он понимал, что, двигаясь дальше, можно оценить
число простых чисел, не превосходящих , и наметил утверждение, которое
затем докажут в XIX в. математики П. Л. Чебышев и Ж. Адамар. Эйлер
много работает в области математического анализа. Здесь он постоянно
пользуется комплексными числами. Его имя носит формула Ученый
впервые разработал общее учение о логарифмической функции, согласно которому
все комплексные числа, кроме нуля, имеют логарифмы, причем каждому числу
соответствует бесчисленное множество значений логарифма. В
геометрии Эйлер положил начало совершенно новой области исследований, выросшей
впоследствии в самостоятельную науку – топологию. Имя
Эйлера носит формула, связывающая число вершин (В), ребер (Р) и граней (Г)
выпуклого многогранника: . Даже
основные результаты научной деятельности Эйлера трудно перечислить. Здесь и
геометрия кривых и поверхностей, и первое изложение вариационного исчисления
с многочисленными новыми конкретными результатами. У него были труды по
гидравлике, кораблестроению, артиллерии, геометрической оптике и даже по
теории музыки. Он впервые дает аналитическое изложение механики вместо
геометрического изложения Ньютона, строит механику твердой точки или твердой
пластины. Одно
из самых замечательных достижений Эйлера связано с астрономией и небесной
механикой. Он построил точную теорию движения Луны с учетом притяжения не
только Земли, но и Солнца. Это пример решения очень трудной задачи. Последние
17 лет жизни Эйлера были омрачены почти полной потерей зрения. Но он
продолжал творить так же интенсивно, как в молодые годы. Только теперь он уже
не писал сам, а диктовал ученикам, которые проводили за него наиболее
громоздкие вычисления. Для
многих поколений математиков Эйлер был учителем. По его математическим
руководствам, книгам по механике и физике училось несколько поколений.
Основное содержание этих книг вошло и в современные учебники. Итак,
определены важнейшие понятия интегрального исчисления и получена формула
Ньютона-Лейбница, связывающая интегрирование и дифференцирование. Подобно
тому как в дифференциальном исчислении к понятию производной вела не только
задача определения мгновенной скорости движения, но и задача проведения
касательной, так в интегральном исчислении к понятию интеграла приводит не
только физическая задача определения пройденного пути по заданной скорости
движения, но и многие другие задачи, и в их числе древние геометрические задачи
о вычислении площадей и объемов. Пусть
требуется найти площадь изображенной на рис. 1 фигуры (называемой
криволинейной трапецией), верхняя «сторона» которой есть график заданной на
отрезке функции
. Точками
разобьем
отрезок на
мелкие отрезки ,
в каждом из которых фиксируем некоторую точку . Площадь узкой криволинейной трапеции,
лежащей над отрезком , заменим приближенно площадью соответствующего
прямоугольника с основанием и высотой . В таком случае
приближенное значение площади всей фигуры даст знакомая нам
интегральная сумма , а точное значение искомой площади получится как
предел таких сумм, когда длина наибольшего из отрезков разбиения
стремится к нулю. Таким образом, получаем: Попробуем
теперь вслед за Архимедом выяснить, в каком отношении парабола делит площадь
изображенного на рис. 2 единичного квадрата. Для этого попросту вычислим,
исходя из формулы (8), площадь нижнего параболического треугольника.
В нашем случае и
. Нам
известна первообразная функции , значит, можно воспользоваться
формулой (7") Ньютона-Лейбница и без труда получить Следовательно,
парабола делит площадь квадрата в отношении 2:1. При
обращении с интегралами, особенно применяя формулу Ньютона-Лейбница, можно
пользоваться общими свойствами неопределенного интеграла, которые названы в
начале статьи. В частности, правило замены переменной в неопределенном
интеграле при условии, что , , с учетом формулы Ньютона-Лейбница
позволяет заключить, что и
таким образом, получается очень полезная формула замены переменной в
определенном интеграле: С
помощью интегралов вычисляют также объемы тел. Если изображенную на рис. 1
криволинейную трапецию вращать вокруг оси , то получится тело
вращения, которое приближенно можно считать составленным из узких цилиндров
(рис. 3), полученных при вращении соответствующих прямоугольников. Сохраняя
прежние обозначения, записываем объем каждого из этих цилиндров в виде (произведение
площади основания
на высоту ).
Сумма дает
приближенное значение объема рассматриваемого тела вращения.
Точное значение получится
как предел таких сумм при . Значит, В
частности, чтобы вычислить объем изображенного на рис. 4 конуса, достаточно
положить в формуле (10) , и , где - угловой коэффициент вращаемой
прямой. Найдя первообразную функции и воспользовавшись формулой Ньютона-Лейбница,
получаем где
площадь
круга, лежащего в основании конуса. В
разобранных примерах мы исчерпывали геометрическую фигуру такими фигурами,
площади или объемы которых могли вычислить, а затем делали предельный переход.
Этот прием, идущий от Евдокса и развитый Архимедом, называется методом
исчерпывания. Это наиболее распространенный метод рассуждений в большинстве
применений интеграла. «Поскольку бочки связаны с
кругом, конусом и цилиндром – фигурами правильными, тем самым они поддаются
геометрическим изменениям». И. Кеплер Смысл – там, где змеи интеграла.
Меж цифр и букв, меж и ! В. Я. Брюсов Открытый урок по алгебре и началам анализа в 11 классе с расширенным изучением математики и физики
«Применение методов математического анализа при решении практических задач».
Учитель: Вишневская Н.В.
Цели урока: 1. Повторить основные типы задач, решаемые методами математического анализа.
2. Повторить алгоритмы решения. 3. Разобрать решение задач повышенной трудности. 4. Решить экономические задачи. План проведения урока: На доске разбираются две задачи повышенной трудности (карточки № 7 и № 5). Пока ребята готовятся, класс устно отвечает на вопросы: а) Области, где применяются методы математического анализа; б) алгоритм решения задач методом поиска наибольших и наименьших значений функции; в) алгоритм решения задач с помощью определенного интеграла. В это же время 6 человек работают по карточкам (№ 3, 4, 6, 8, 9, 10). Заполняются таблицы. Проверяются задачи на доске, учитель проверяет правильность решения задач по карточкам. Разбирается на доске экономическая задача (карточка № 1, 2). Домашняя контрольная работа. Алгоритм решения задач методом поиска наибольших и наименьших значений функции. Алгоритм вычисления геометрических и физических величин с помощью определенного интеграла. Выражают искомую величину как значение в некоторой точке в функции F
.
Находят производную f
этой функции.
Выражают функцию F
в виде определенного интеграла от f
и вычисляют его.
Подставляя значение х
= b
находят искомую величину.
Домашние задачи (на доске):
Два корабля движутся по двум перпендикулярным прямым, пересекающимся в точке О
, по направлению к О
. В какой-то момент времени оба находятся в 65 км от О
, скорость первого равна 15 км/ч, второго – 20 км/ч. От первого корабля отходит моторная лодка, движущаяся со скоростью 25 км/ч.
а) За какое наименьшее время катер может доплыть от первого корабля до второго?
б) За какое наименьшее время катер может доплыть от первого корабля до второго и вернуться обратно на первый корабль?
V
1 = 15 км/ч
65 км S
1 О
S
3 S
2
65 км
V
л = 25 км/ч
V
2 = 20 км/ч
Решение:
х
– время, которое прошло от того момента, когда оба корабля находились в 65 км от О
, до момента отправления катера.
В момент отправления катера 1-й корабль был на расстоянии Продифференцируем по х
:
Ответ: а) 1 час; б) 3 часа.
Котел имеет форму параболоида вращения. Радиус его основания R
= 3 м, глубина Н
= 5 м. Котел наполнен жидкостью, удельный вес которой 0,8 Г/см 3 . Вычислить работу, которую нужно произвести, чтобы выкачать жидкость из котла.
у
у
R
= 3 м
Н
= 5 м
уд. вес = 0,8 Г/см 3
Вычислить работу, которую нужно произвести, чтобы выкачать жидкость из котла.
Решение:
В плоскости сечения хОу
АОВ
– парабола, уравнение которой Координаты точки В
должны удовлетворять этому уравнению, т.е.
Разделим параболоид на слои плоскостями, параллельными поверхности жидкости. Пусть толщина слоя на глубине (Н
– у)
равна dy
. Тогда, принимая приближенно слой за цилиндр, получим его объем Из уравнения параболы Следовательно, чтобы выкачать жидкость с глубины Ответ: Работа в классе.
Какую работу нужно затратить, чтобы растянуть пружину на 6 см, если сила 1 кГ растягивает ее на 1 см?
Решение:
Согласно закону Гука сила F
кГ, растягивающая пружину на х
, равна х
= 0,01 м
F
= 1 кГ
Тогда Искомая работа Ответ: 0,18 кГм.
Вычислить работу силы F
при сжатии пружины на 5 см, если для сжатия ее на 1 см нужна сила в 1 кг.
Решение:
По закону Гука х
= 0,01 м
F
= 1 кГ
Тогда Искомая работа Ответ: 0,125 кГм.
Сила F
, с которой электрический заряд где k
– постоянная.
Определить работу силы F
при перемещении заряда Решение:
Работа определяется по формуле При Ответ: Определить силу давления воды на вертикальную стенку, имеющую форму полукруга радиуса R
= 6 м, диаметр которого находится на поверхности воды.
Решение:
Сила давления жидкости на площадку площадью S
при глубине погружения х
равна х С
dх
А В
Полукруг параллельными прямыми разделим на полоски, которые примем за прямоугольник. Пусть заштрихованная полоска имеет длину АВ
, ширину dx
и находится на глубине х
Давление воды на полоску, находящуюся на глубине х
, будет равно .
Отсюда Удельный вес воды 1 см 3 = 1 Г, следовательно вес 1м 3 = 1000 кГ.
1 кГ 1 бар = 0,987 атм.
Ответ: 144000 кГ.
Скорость движения точки Решение:
Следовательно Ответ: 512 м; 64 м/сек.
Карточка № 1 (решается в классе на доске)
Средние совокупные издержки производства мыла Связь между годовым объемом продаж, равным величине годового выпуска Q
, и ценой мыла Р
(в тыс. рублей за тонну) описывается формулой
Реализовав по фиксированной цене все сваренное за год мыло, завод получил максимально возможную прибыль. Какова была при этом выручка предприятия?
Решение:
Выразим через Q
сначала цену мыла из формулы Тогда прибыль G
можно выразить:
Найдем критические точки этой функции:
Критические точки 100, –340, –120.
Отрицательные корни не имеют экономического смысла.
Q
G
Значит оптимальный годовой объем мыла Тогда годовая выручка R
составит: (тыс. руб.).
Ответ: 1 млн. руб.
Найти величину давления воды на прямоугольник, вертикально погруженный в воду, если известно, что его основание равно 8 м, высота 12 м, верхнее основание параллельно поверхности воды и находится на глубине 5 м.
Решение:
5 м
8 м
х
dx
12 м
кГм.
Ответ: Карточка № 2 (дополнительная)
Производственные мощности позволяют предприятию «Линотрон» выпускать не более 600 тонн ваты в год. Зависимость величины совокупных издержек Связь между годовым объемом продаж ваты, который совпадает с объемом годового производства, и ценой на вату Р
(в тыс. рублей за тонну) описывается функцией
Цена на вату устанавливается 1 января 1995 года и пересматривается лишь 1 января следующего года.
Найдите с точностью до 1 % рентабельность производства по издержкам, если за 1995 год предприятие получит максимально возможную прибыль.
Решение:
Используя зависимости у у a
0 b c x a
0 b c x
Введение
![]() .
.
![]() . (поверхность визуализирована в задаче 2).
. (поверхность визуализирована в задаче 2).
 , где .
, где .![]() ,
,  ,
, ![]() ,
,  ,
,  , где .
, где .![]() , где S
- сфера
, где S
- сфера ![]() (по теореме 3).
(по теореме 3).
![]()
![]() , отличающаяся от постоянным слагаемым : ведь
, отличающаяся от постоянным слагаемым : ведь ![]() .
.![]() , (1)
, (1)![]() ;
;
![]() ;
; ![]() .
.![]() ,
,
![]() ,
, ![]() ,
, ![]() .
.![]()
![]() ,
,
![]() , (3)
, (3)![]()


 (5)
(5) . (6)
. (6)![]() функции по формуле (7), получаем величину
функции по формуле (7), получаем величину
 (6")
(6") . (7)
. (7)
(1707-1783)

![]() , устанавливающая связь
тригонометрических и показательной функций, возникающую при использовании
комплексных чисел.
, устанавливающая связь
тригонометрических и показательной функций, возникающую при использовании
комплексных чисел.
 .
.
 . (9)
. (9) . (10)
. (10)



Карточка № 7
 – время, которое необходимо катеру на путь от 1-го корабля до 2-го.
– время, которое необходимо катеру на путь от 1-го корабля до 2-го.
 км от О
; в момент прибытия катера на 2-ой корабль, расстояние между ним и О
было равно км; путь катера равен
км от О
; в момент прибытия катера на 2-ой корабль, расстояние между ним и О
было равно км; путь катера равен  . Тогда по теореме Пифагора
. Тогда по теореме Пифагора
 .
.


 ;
; 
 ;
; 
Карточка № 5
![]()
 А
R
В
А
R
В


 dy
Н
dy
Н

О х х
 . Найдем параметр а
.
. Найдем параметр а
.
 ,
,
 , следовательно
, следовательно  .
.
 .
.
 , тогда
, тогда  , т.е. вес слоя жидкости равен
, т.е. вес слоя жидкости равен 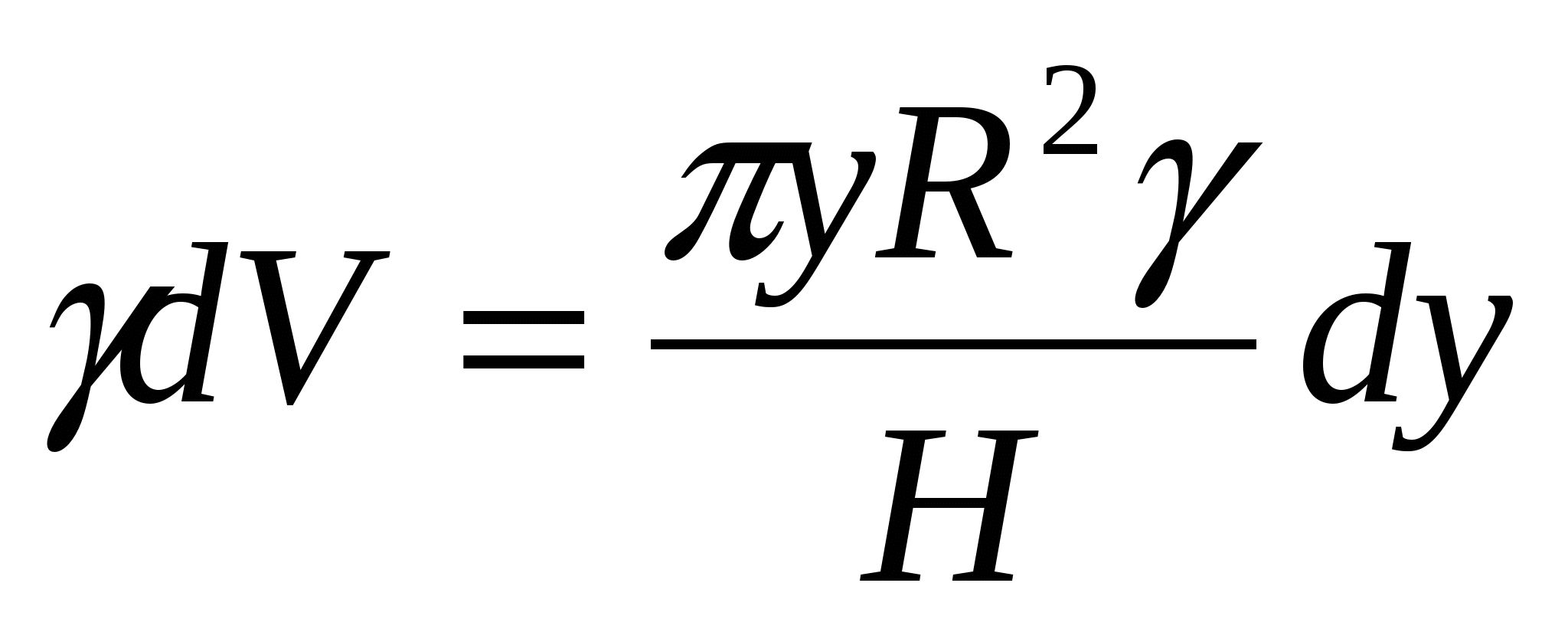 .
.
 , потребуется затратить элементарную работу
, потребуется затратить элементарную работу  ,
,  . Тогда
. Тогда
 , тогда .
, тогда .
 .
.
Карточка № 6
 , k
– коэффициент пропорциональности.
, k
– коэффициент пропорциональности.
 , следовательно
, следовательно  .
.
 .
.
Карточка № 8
 .
.
 , следовательно
, следовательно  .
.
 .
.
Карточка № 9
 отталкивает заряд
отталкивает заряд  (того же знака), находящийся от него на расстоянии r
, выражается формулой
(того же знака), находящийся от него на расстоянии r
, выражается формулой
 ,
,
 из точки
из точки  , отстоящей от
, отстоящей от  на расстоянии
на расстоянии  , в точку
, в точку  , отстоящую от
, отстоящую от  на расстоянии
на расстоянии  , полагая, что заряд
, полагая, что заряд  помещен в точке
помещен в точке  , принятой за начало отсчета.
, принятой за начало отсчета.
 ,
,  . Тогда
. Тогда
 .
.
 получим
получим  .
.
 .
.
Карточка № 3
 ,
,  – удельный вес жидкости.
– удельный вес жидкости.
О

 .
.

 ,
,
 ,
,
 ,
,

 .
.
 ;
;
 9,81 н
9,81 н
Карточка № 4
 м/сек. Найти путь s
, пройденный точкой за время Т
= 8 сек после начала движения. Чему равна средняя скорость движения за этот промежуток?
м/сек. Найти путь s
, пройденный точкой за время Т
= 8 сек после начала движения. Чему равна средняя скорость движения за этот промежуток?
 , следовательно
, следовательно  ,
,  ,
,  .
.
 .
.
 .
.
 (в тыс. рублей на тонну) на Мухинском мыловаренном заводе изменяются в зависимости от объема годового выпуска Q
(в тоннах) по закону:
(в тыс. рублей на тонну) на Мухинском мыловаренном заводе изменяются в зависимости от объема годового выпуска Q
(в тоннах) по закону:
 .
.
 .
.
 .
.
 .
.
 ,
,  .
.



 ;
;
 .
.
 т, тогда цена
т, тогда цена  (тыс. руб./т).
(тыс. руб./т).
Карточка № 10
 ,
,  ,
,  м.
м.
 .
.
 кГм.
кГм.
 (в тыс. рублей) от годового объема производства Q
(в тоннах) имеет вид
(в тыс. рублей) от годового объема производства Q
(в тоннах) имеет вид
 .
.
 и , выразим
.
и , выразим
.
















